CSC3001 Discrete Mathematics
L0 Introduction
Main Course Topics
- Propositional Logic
- Sets, First-Order Logic
- Methods of Proofs
- Mathematical Induction
- Recursion
- Greatest Common Divisors
- Modular Arthmetic
- Chinese Remainder Theorem
- Graphs
- Graph Matching
- Graph Coloring
- Combinatorial Proofs and its Principles
- Counting by Mapping
- Cardinality
L1 Propositional Logic
Statement (Proposition)
A Statement is a sentence that is either True or False.
e.g. $2+2=4 \to \text{True}$
Non e.g. $x+y>0$, cause they are true for some values of $x$ and $y$, but false for others.
Logic Operators
NOT $\lnot$
Alternative notation: $\lnot P = \overline{P}$
| $P$ | $\lnot P$ |
|---|---|
| T | F |
| F | T |
AND $\land$
| $P$ | $Q$ | $P\land Q$ |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
OR $\lor$
| $P$ | $Q$ | $P\lor Q$ |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
XOR $\oplus$
Exclusive OR
| $P$ | $Q$ | $P\oplus Q$ |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
De Morgan's Laws
Logical Equivalence: Two statements have the same truth table.
De Morgan's Laws:
$$ \lnot (P \land Q) \equiv \lnot P \lor \lnot Q $$ $$ \lnot (P \lor Q) \equiv \lnot P \land \lnot Q $$
Tautology and Contradiction
A tautology is a statement that is always true.
- e.g. $P \lor \lnot P$
A contradiction is a statement that is always false. (Negation of a tautology)
- e.g. $P \land \lnot P$
Conditinal Statement
If $\to$
If P then Q: $P \to Q \equiv \lnot P \lor Q$
| $P$ | $Q$ | $P \to Q$ |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Convention: If we don't say anything wrong, then it is not false, and thus true.
Negation of If-Then: $\lnot(P \to Q) \equiv P \land \lnot Q$
Contrapositive: The contrapositive of $P \to Q$ is $\lnot Q \to \lnot P$
$$ P \to Q \equiv \lnot P \lor Q \equiv Q \lor \lnot P \equiv \lnot Q \to \lnot P $$
If and Only If $\iff$
P if Q means "if Q then P", or "Q implies P". We also say Q is a sufficient condition for P.
P only if Q means "if P then Q", or "P implies Q". We also say Q is a necessary condition for P.
P if and only if (iff) Q means P and Q are logically equivalent.
| $P$ | $Q$ | $P \iff Q$ |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
$$ P \iff Q \equiv (P \to Q) \land (Q \to P) \equiv (P \to Q) \land (\lnot P \to \lnot Q) $$
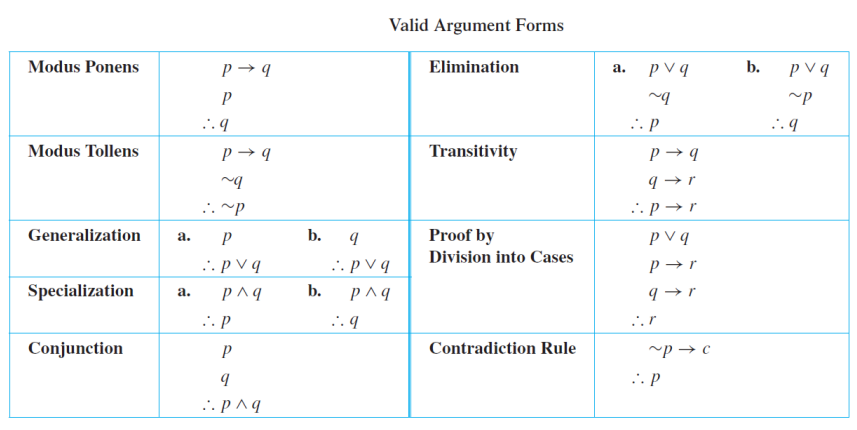
Argument
An argument is a sequence of statements.
All statements but the final one are called assumptions or hypothesis.
The final statement is called the conclusion.
An argument is valid if: whenever all the assumptions are true, then the conclusion is true. Or we say the conclusion follows from the assumptions.
L2 Sets
Basic Definitions
Defining Sets
Set: A set is an unordered collection of distinct objects.
Elements / Members: The objects in a set are called the elements or members of the set S, and we say S contains its elements.
e.g. $S=\{2,3,5,7\} = \{3,7,2,5\}$ (Unordered)
Alternatively, we use the notation $\{x \in A | P(x)\}$ to define the set as the set of elemets, $x$, in $A$ such that $x$ satisfies property $P$.
Classical Sets
- $\mathbb{Z}$: The set of all integers
- $\mathbb{Z^+}$: The set of all positive integers
- $\mathbb{Z^-}$: The set of all negative integers
- $\mathbb{N}$: The set of all nonnegative integers
- $\mathbb{R}$: The set of all real numbers
- $\mathbb{Q}$: The set of all rational numbers
- $\mathbb{C}$: The set of all complex numberse
Membership
The most basic question in set theory is whether an element is in a set.
- $A \subseteq B$: $A$ is an subset of $B$
- $A = B$: $A$ is equal to $B$
- $A \subset B$: $A$ is an proper subset of $B$
Operations on Sets
Basic Operations on Sets
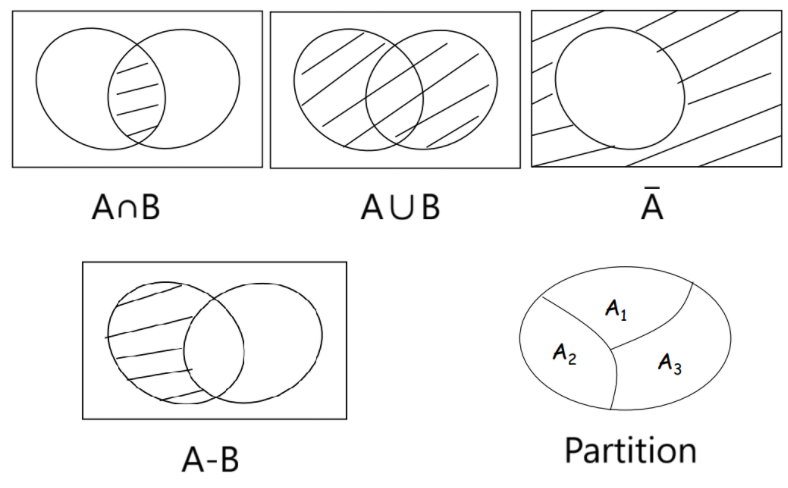
Intersection: $A \cap B = \{x \in U | x \in A \text{ and } x \in B\}$
Two sets are said to be disjoint if their intersection is an empty set.
Union: $A \cup B = \{x \in U | x \in A \text{ or } x \in B\}$
And we have $|A \cup B| = |A|+|B| - |A \cap B|$
Complement: $\overline{A} = A^c = \{x \in U | x \notin A\}$
And if $A \subseteq B$, then $\overline{B} \subseteq \overline{A}$
Difference: $A - B = \{ x \in U | x \in A \text{ and }x \notin B \}$
And we have $|A-B| = |A| - |A \cap B|$
Big set operators: $$ \begin{align*} \bigcup_{i=0}^n A_i &= \{ x \in A_i \text{ for at least one } i = 0, 1, 2, \cdots, n \} \\ \bigcap_{i=0}^n A_i &= \{ x \in A_i \text{ for all } i = 0, 1, 2, \cdots, n \} \end{align*} $$
Partition of Sets
Partition: A collection of nonempty sets $\{ A_1, A_2, \cdots, A_n \}$ is a partition of a set A if and only if $$ \begin{align*} & A = A_1 \cup A_2 \cup \cdots \cup A_n \\ & A_1, A_2, \cdots, A_n \text{ are mutually disjoint (or pairwise disjoint)} \end{align*} $$
Cartesian Products
Cartesian Products: Given two sets $A$ and $B$, the Cartesian product $A \times B$ is the set of all ordered pairs $(a,b)$, where $a$ is in $A$ and b is in $B$. That is: $$ A \times B = \{(a,b) | a \in A, b \in B\} $$
e.g. Let $A = \{ a, b, c, \cdots, z \}$. Let $B = \{ 0, 1, 2, \cdots, 9 \}$. Then $A \times B = \{ (a,1), (a,2), \cdots, (a, 9), (b, 1), (b, 2), \cdots, (z, 9) \}$
Well...It may seems a bit like the outer product of two vectors is a matrix, but in a set.
Set Identities
Set Laws
Let $A$, $B$ and $C$ be subsets of a universal set $U$, and we have:
- Commutative Law
- $A \cup B = B \cup A$
- $A \cap B = B \cap A$
- Associative Law
- $(A \cup B) \cup C = A \cup (B \cup C)$
- $(A \cap B) \cap C = A \cap (B \cap C)$
- Distributive Law
- $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
- $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
- Identity Law
- $A \cup \emptyset = A$
- $A \cap U = A$
- Complement Law
- $A \cup A^c = U$
- $A \cap A^c = \emptyset$
- De Morgan's Law
- $(A \cup B)^c = A^c \cap B^c$
- $(A \cap B)^c = A^c \cup B^c$
- Set Difference Law
- $A - B = A \cap B^c$
L3 First-order Logic
Quantifiers
Predicates
Predicate: Propositions (i.e. statments) with variables.
- e.g. $P(x, y): x + 2 = y$
The domain of a variable is the set of all values that may be substituted in place of the variable.
The truth of a quantified statement depends on the domain.
The Universal Quantifier $\forall$
$\forall x$: For ALL $x$
- e.g. $\forall x, x^2 \geq x$
The Existential Quantifier $\exists$
$\exists x$: There EXISTS some $x$ (perhaps one)
- e.g. $\exists x \in \mathbb{Z}^+, x=x^2$
e.g. How to write prime(p) ?
A prime number is a natural number greater than $1$ that has no positive divisors other than $1$ and itself.
- Conditions: $p \not= ab$
- Variables: $p, a, b$
- Domains: $p, a, b > 1, p, a, b \in \mathbb{Z}$
- Add quantifiers and reconcile the order:
$$ (p > 1) \land (p \in \mathbb{Z}) \land (\forall a, b, \in \mathbb{Z}^+, (p \not= ab) \lor (a=1) \lor (a=p)) $$
Negation
One simple equivalence: $$ \lnot \forall x, P(x) \equiv \exists x, \lnot P(x) $$ e.g. Not every like you = There exists someone who doesn't like you.
Multiple Quantifiers
The order of quantifiers is very important.
Arguments of Quantified Statements
Predicate Calculus Validity

A quantified argument is valid if the conclusion is true whenever the assumptions are true.
Arguments with Quantified Statements
Universal Instantiation: $$ \begin{align*} & \forall x , P(x) \\ \therefore \ & P(a) \end{align*} $$
Universal Modus Ponens $$ \begin{align*} & \forall x , (P(x) \to Q(x)) \\ & P(a) \\ \therefore \ & Q(a) \end{align*} $$
Universal Modus Tollens: $$ \begin{align*} & \forall x, P(x) \to Q(x) \\ & \lnot Q(A) \\ \therefore \ & \lnot P(A) \end{align*} $$
Universal Generalization: $$ \frac{A \to R(c)}{A \to \forall x , R(x)} \qquad \\ \text{(valid rule, provided $c$ is independent of $A$)} $$